点“考研竞赛数学”↑可每天“涨姿势”哦!
壹
与函数不等式证明相关的导数知识点
一、函数单调性的判定
设函数f(x)在[a,b]上连续,在(a,b)内可导,则
(1)在(a,b)内f’(x)>0,则函数f(x)在[a,b]上严格单调增加.
(2)在(a,b)内f’(x),则函数f(x)在[a,b]上严格单调减少.
二、函数极值第一充分条件
设f(x)在x0处连续,在x0的某去心邻域内可导,则
(1)如果f’(x)左正右负,那么f(x)在x0处取极大值.
(2)如果f’(x)左负右正,那么f(x)在x0处取极小值.
(3)如果f’(x)不变号,那么f(x)在x0处不取极值.
三、极值的第二充分条件
设函数f(x)在x0处具有n阶导数,且
那么
(1) n为偶数时,x0为极值点,且n阶导数大于0,取极小值;n阶导数小于0,取极大值.
(2) n为奇数时,x0不是极值点.
四、凹凸性相关的不等式结论
(1)设函数f(x)在区间I上连续,若f(x)的图形是凹的,则有
若f(x)的图形是凸的,则有
(2)如果在曲线y=f(x)上任意一点(x0, f(x0))作切线,那么,凹曲线位于切线上方,凸曲线位于切线下方,即有
五、函数图形凹凸性的判定
设f(x)在(a,b)内存在二阶导数,
(1)如果在(a,b)内f’’(x)>0,则f(x)描述的曲线为凹弧;
(2)如果在(a,b)内f’’(x),则f(x)描述的曲线为凸弧.
六、最值定理
如果f(x)在[a,b]内连续,则必在该区间上取到最大值和最小值,即存在c,d∈[a,b],有
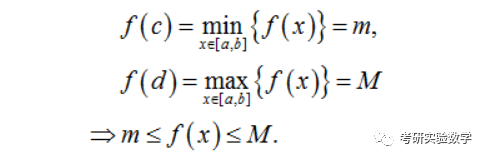
七、闭区间上的连续函数最值求解步骤
(1)求出函数在闭区间上的所有导数等于零的点(驻点)和导数不存在的点;
(2)求出函数在以上各点的函数值与端点的取值.
(3)比较以上各值的大小,最大的为最大值,最小的为最小值.
贰
典型题解析
例:证明:当0时,有
证明1:(利用函数图形的凹凸性证明)令
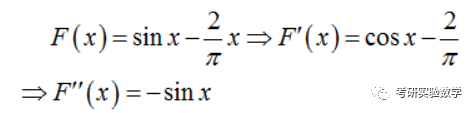
当0时,F’’(x),所以函数F(x)的图形为严格的凸曲线,从而有
所以结论成立.
证明2:(利用函数的单调性证明)由于0,所以
于是令
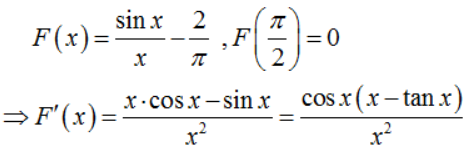
由于0时,0,所以可得F’(x),由此可知函数F(x)在区间0上严格单调递减.由于右端点等于零,所以函数F(x)>0,从而可知结论成立.
证明3:(利用最值不等式)令
由此可知函数F(x)在闭区间[0,π/2]上为连续函数,因此有最大值M和最小值m.令
在(0,π/2)只有唯一的极值点,且F(0)=F(π/2)=0,结合当0时,F’’(x),函数F(x)的图形为严格的凸曲线,所以x=x0取到极大值,也即函数的最大值,并且最大值是一个大于0的数,所以函数F(x)的最大值为F(x0),最小值为0,从而当0时,有
所以结论成立.








添加新评论